리트코드 85번 문제
Given a rows x cols binary matrix filled with 0's and 1's, find the largest rectangle containing only 1's and return its area.
Example 1:
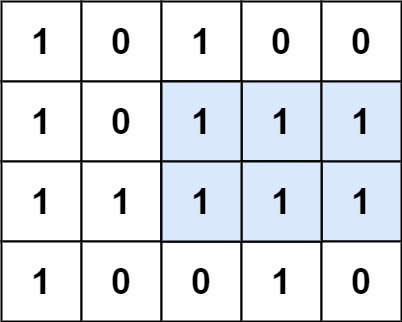
- Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
- Output: 6
- Explanation: The maximal rectangle is shown in the above picture.
Example 2:
- Input: matrix = [["0"]]
- Output: 0
Example 3:
- Input: matrix = [["1"]]
- Output: 1
Constraints:
- rows == matrix.length
- cols == matrix[i].length
- 1 <= row, cols <= 200
- matrix[i][j] is '0' or '1'.
주어진 행렬에서 '1'로 구성된 가장 큰 직사각형을 구하는 문제로 이전에 풀었던 84번 문제와 풀이방식이 같다.
다만, 행을 순회하면서 각 열에 대한 연속된 '1'의 길이를 업데이트 한다. 1번 예시로 보면 다음과 같다.
| 1 | 0 | 1 | 0 | 0 |
| 2 | 0 | 2 | 1 | 1 |
| 3 | 1 | 3 | 2 | 2 |
| 4 | 0 | 0 | 3 | 0 |
그리고 각 행에서 heights 배열 업데이트를 마치고 나면 히스토그램에서 최대 직사각형의 넓이를 찾기 위해 stack 자료구조를 사용하는 데 이 부분은 84번 문제 풀이와 같다. 84번 문제를 풀었을 때는 마지막에 stack에 남아있는 요소를 꺼내서 처리했는데, 여기서는 k == col로 heights 배열에 마지막에 도달했을 때 별도 처리하는 식으로 하여 코드를 간결하게 하고 stack의 범위를 루프 안에 둬서 굳이 비워줄 필요가 없게 했다.
class Solution {
public:
int maximalRectangle(vector<vector<char>>& matrix) {
int row = matrix.size();
int col = matrix[0].size();
int maxArea = 0;
vector<int> heights(col, 0);
for(int i = 0; i < row; i++) {
for(int j = 0; j < col; j++) {
if(matrix[i][j] == '1') heights[j]++;
else heights[j] = 0;
}
stack<int> st;
for(int k = 0; k <= col; k++) {
int currHeight = (k == col) ? 0 : heights[k];
while(!st.empty() && currHeight < heights[st.top()]){
int height = heights[st.top()];
st.pop();
int width = st.empty() ? k : k - st.top() - 1;
maxArea = max(maxArea, height * width);
}
st.push(k);
}
}
return maxArea;
}
};
'코딩테스트' 카테고리의 다른 글
| Python ] leetCode 1861 - Rotating the Box (0) | 2024.06.02 |
|---|---|
| Python ] leetCode 189 - Rotate Array (0) | 2024.05.31 |
| C++ ] leetCode 84 - Largest Rectangle in Histogram (0) | 2024.05.18 |
| C++ ] leetCode 42 - Trapping Rain Water (0) | 2024.05.14 |
| C++ ] leetCode 937 - Reorder Data in Log Files (0) | 2024.05.10 |



