아날로그 필터 (Analog Filter)
회로에서 저항(R), 커패시터(C), 인덕터(L) 등의 수동 소자 또는 연산 증폭기(Op-Amp)를 활용하여 구현하는 필터이다. 하드웨어적으로 신호를 직접 처리하며, 대표적인 예로 LPF(Low Pass Filter), HPF(High Pass Filter), BPF(Band Pass Filter), BSF(Band Stop Filter) 등이 있다.
디지털 필터 (Digital Filter)
디지털 필터는 아날로그 구성요소를 사용하는 대신 주로 소프트웨어 구현을 통해 특정 주파수 대역의 신호를 남기고 원하지 않는 대역의 신호를 감쇠시킨다. 구현에는 ADC로 아날로그 신호를 샘플링한 다음 소프트웨어 알고리즘을 적용하는 것이 포함된다.
대표적인 방식으로 FIR(Finite Impulse Response) 필터와 IIR (Infinite Impulse Response) 필터가 있다.
🔍 임펄스(Impulse)란?
임펄스(Impulse)란 순간적으로 발생하는 강한 신호로, 디지털시스템에서는 단일샘플이 1이고 나머지 값이 0인 수열이다.

FIR (유한 임펄스 응답) 필터
FIR 필터는 유한한 개수의 샘플을 사용하여 출력을 생성하는 디지털 필터이다. 대표적인 예로 이동 평균 필터를 들 수 있다. 예를 들어, 10포인트 이동 평균 필터는 최근 10개의 입력 값을 평균 내어 출력을 생성한다. 입력 신호에 1이 등장하면 출력은 0.1 값을 유지하다가 10번의 샘플이 지난 후 0이 된다. 이는 FIR 필터가 제한된 개수의 샘플 내에서 신호를 처리하기 때문이며, 이러한 특성을 유한한 길이의 임펄스 응답을 가진다고 표현한다.
IIR (무한 임펄스 응답) 필터
IIR 필터는 과거의 입력 값이 지속적으로 현재의 출력에 영향을 미치는 유형의 디지털 필터이다. 대표적인 예로 지수 이동 평균 필터를 들 수 있다. 이 필터는 과거 샘플 값에 지수적으로 감소하는 가중치를 적용하여 출력을 생성한다. 입력 신호에 1이 등장하면 시간이 지나면서 출력은 무한히 0에 가까워지지만 완전히 0이 되지는 않는다. 즉, 과거의 입력 값이 지속적으로 현재 출력에 영향을 미치며 이러한 특성을 무한 임펄스 응답이라고 한다.
Moving Average 필터
이동 평균 필터는 고주파 잡음을 제거하고 신호를 부드럽게(Smoothing)만드는 가장 간단한 필터 중 하나이다.
이동 평균 필터는 주어진 신호에서 일정 구간의 평균을 구해 새로운 신호를 만드는 방법으로 그 수식은 다음과 같다.

- y[n] : 출력 신호 (필터링된 신호)
- x[n] : 입력 신호
- N = Window Size (평균을 낼 샘플 개수)
N = 3인 경우, 최근 3개의 값을 평균 내어 새로운 값을 생성하며, 입력신호 x[n]에 대해 출력 신호 y[n]은 다음과 같이 계산된다.
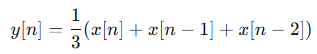
이동 평균 필터에서 윈도우 사이즈(Windows Size, N)은 필터링된 출력을 계산할 때 평균을 내는 샘플 개수를 의미한다. 윈도우 사이즈에 따른 이동 평균 필터의 차이를 보면 다음과 같다.

- 윈도우 사이즈가 작을 수록 노이즈 제거 효과는 적지만 신호 변화에 빠르게 반응한다.
- 윈도우 사이즈가 클수록 노이즈 제거 효과가 강하지만 edge가 퍼지면서 변동성이 줄어든다.
윈도우 사이즈가 5와 11인 이동 평균 필터의 주파수 응답을 보면 다음과 같다.
아래 그래프의 y축은 주파수 응답의 Magnitude의 제곱값을 dB스케일로 나타낸 것이고 x축은 정규화된 주파수 범위(-fs/2 ~ fs/2)를 의미한다.
윈도우 사이즈가 11인 필터가 5인 필터에 비해 더 낮은 주파수만 통과시키고, 높은 주파수를 더 많이 감쇠시키는 것을 볼 수 있다.
한편 이동 평균 필터의 주파수 응답은 고주파를 급격하게 차단하는 경향이 있지만 정지 대역에서는 반복적인 리플(Ripple)이 발생하여 고주파 성분이 완전히 제거되지 않는 문제가 있다. 이러한 특성으로 인해 이동 평균 필터는 시간 영역에서는 좋은 스무딩 필터지만, 주파수 영역에서는 이상적인 LPF로 사용하기에는 한계가 있다.

또한 Moving Average 필터의 특징 중 하나는 아래의 Exponential 필터와 달리 주파수에 따라 선형적으로 증가하는 위상 지연을 가지며, 실제로 시간 도메인에서는 모든 주파수 성분이 동일한 시간 지연을 겪게 된다는 점이다.
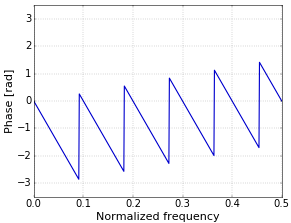
The Phase Response of a Filter | TomRoelandts.com
The Phase Response of a Filter
tomroelandts.com
Exponential 필터
앞에서 살펴본 Moving Average 필터의 단점은 모든 샘플에 동일한 가중치를 적용한다는 점이다. 만약 최근 샘플에 더 많은 가중치를 주고 싶다면 Exponential 필터를 사용할 수 있다.
Exponential 필터의 수식은 다음과 같다.
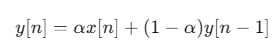
- y[n] : 출력 신호
- x[n] : 현재 입력 샘플
- y[n-1] : 이전 출력 신호
- α : 현재 샘플의 가중치 (0 < α < 1, α = 0.9이면 현재값 90%, 이전값 10%)
이 필터는 이전 입력의 기여도가 시간이 지날수록 지수적으로 감소하기 때문에 지수 가중 평균 필터라고 불린다.
Exponential 필터의 alpha 값 설정에 따른 변화를 보면 다음과 같다.

- alpha 값이 작을 수록 노이즈 제거 효과가 강하지만 신호가 둔하게 변화하여 지연이 생길 수 있다.
- alpha 값이 클수록 최근 데이터의 영향을 많이 받아서 빠르게 반응한다.
다음은 alpha 값이 0.25일 때와 0.75일 때의 주파수 응답 그래프이다. Moving Average 필터보다는 완만한 형태로 감쇠되는 특성을 가지는 것을 볼 수 있다. 또한 Exponential 필터의 특징 중 하나는 주파수 성분에 따라 위상 지연이 비선형적으로 발생한다는 점이다.

- alpha 값이 작을수록 저역통과 필터 특성이 강하며, 노이즈 제거 효과가 강해 신호가 부드러워지지만 위상 지연이 발생하여 반응속도가 느려진다.
- alpha 값이 클수록 더 높은 주파수까지 그냥 통과되고 노이즈 제거 효과가 약하지만 위상 지연이 적고 빠른 신호 변화를 더 잘 추적한다.
C 테스트 코드
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <stdint.h>
#define PI 3.1415926
#define SAMPLE_SIZE 100
// Moving Average Filter 구조체 정의
typedef struct {
uint8_t index;
uint8_t window_size;
float sum;
float* buffer;
} movingAverageFilter_t;
// Moving Average Filter 초기화 함수
void init_moving_average_filter(movingAverageFilter_t* filter, float* buffer, uint8_t window_size) {
if (filter == NULL || buffer == NULL) return;
filter->index = 0;
filter->window_size = window_size;
filter->sum = 0;
filter->buffer = buffer;
for (int i = 0; i < filter->window_size; i++) {
buffer[i] = 0.0F;
}
}
// Moving Average Filter 적용 함수
float update_moving_average(movingAverageFilter_t* filter, float new_sample) {
if (filter == NULL || filter->buffer == NULL || filter->window_size == 0) return 0.0F;
filter->sum -= filter->buffer[filter->index];
filter->buffer[filter->index] = new_sample;
filter->sum += new_sample;
filter->index = (filter->index + 1) % filter->window_size;
return filter->sum / filter->window_size;
}
// Exponential Filter 함수
float exponential_filter(float prev_value, float new_sample, float alpha) {
return (alpha * new_sample) + ((1 - alpha) * prev_value);
}
int main() {
FILE* fp = fopen("filter_output.csv", "w");
if (!fp) {
printf("파일 저장 오류.\n");
return -1;
}
fprintf(fp, "Time,NoisyPulse,MA_Pulse,EXP_Pulse,Time,NoisySine,MA_Sine,EXP_Sine\n");
float pulse_signal[SAMPLE_SIZE];
float sine_wave[SAMPLE_SIZE];
// 펄스 신호와 사인 웨이브 신호 생성
for (int i = 0; i < SAMPLE_SIZE; i++) {
pulse_signal[i] = (i >= 30 && i < 70) ? 1.0F : 0; // 40%가 HIGH인 펄스 신호
sine_wave[i] = (float)sin(2 * PI * 5.0 * i / SAMPLE_SIZE); // 5주기 사인 웨이브 신호
}
// Moving Average Filter 필터 초기화
movingAverageFilter_t ma_pulse_filter;
float ma_pulse_filter_buffer[10];
init_moving_average_filter(&ma_pulse_filter, ma_pulse_filter_buffer, 10); // 펄스 신호 윈도우 크기 10
movingAverageFilter_t ma_sine_filter;
float ma_sine_filter_buffer[5];
init_moving_average_filter(&ma_sine_filter, ma_sine_filter_buffer, 5); // 사인웨이브 신호 윈도우 크기 5
// Exponential Filter 적용 변수 초기화
float exp_pulse_output = 0;
float exp_sine_output = 0;
for (int i = 0; i < SAMPLE_SIZE; i++) {
// -0.1 ~ 0.1의 노이즈 추가
float noise_pulse = ((rand() / (float)RAND_MAX) * 0.2f) - 0.1f;
float noise_sine = ((rand() / (float)RAND_MAX) * 0.2f) - 0.1f;
float noisy_pulse = pulse_signal[i] + noise_pulse;
float noisy_sine = sine_wave[i] + noise_sine;
// 필터 적용
float ma_pulse_output = update_moving_average(&ma_pulse_filter, noisy_pulse);
exp_pulse_output = exponential_filter(exp_pulse_output, noisy_pulse, 0.3f);
float ma_sine_output = update_moving_average(&ma_sine_filter, noisy_sine);
exp_sine_output = exponential_filter(exp_sine_output, noisy_sine, 0.5f);
// 결과 기록
fprintf(fp, "%d,%.4f,%.4f,%.4f,%d,%.4f,%.4f,%.4f\n",
i, noisy_pulse, ma_pulse_output, exp_pulse_output,
i, noisy_sine, ma_sine_output, exp_sine_output);
}
fclose(fp);
printf("'filter_output.csv' 파일 저장 완료.\n");
return 0;
}

'임베디드 개발 > 펌웨어' 카테고리의 다른 글
| RJ-45 커넥터 핀아웃 (10/100BASE-T, 1000BASE-T 연결 방법) (0) | 2025.04.15 |
|---|---|
| DAC sine wave 생성 (0) | 2025.04.12 |
| 타코미터 센서 (Tachometer) (0) | 2025.03.24 |
| CH341A 프로그래머 사용하기 (0) | 2025.02.24 |
| MDIO ] Clause 22 vs Clause 45 (0) | 2025.01.25 |


