ADC SNR
ADC SNR (Signal to Noise Ratio)
신호와 잡음의 비율을 나타내는 SNR은 ADC 회로 상에서 발생하는 노이즈와 신호의 비율을 나타내기 위해서도 사용한다. 즉, 해당 값이 클수록 설계한 ADC 시스템이 신호에 비해 잡음이 얼마나 적고, 신호를 얼마나 정확하게 전달하는지 나타낸다.
이전 글(https://eteo.tistory.com/917)에서도 설명하였는데 SNR은 신호 수준 대 노이즈 수준의 비에 상용로그를 취한 뒤 20을 곱하여 dB 스케일로 표현한다.

단, ADC SNR을 말할 때의 '노이즈'는 양자화 오류만을 고려한 값이다. 즉, SNR은 내부 회로의 잡음이나 열 잡음, 전자기 간섭으로 인한 잡음 등 추가 잡음원을 고려하지 않고 양자화 오류만을 고려한 이상적인 값으로 ADC 시스템이 가질 수 있는 가장 높은 값이다. 따라서 실제 시스템에서는 여러 비이상적인 요소들로 인해 SNR보다 항상 낮은 성능(낮은 dB값)이 나올 수 밖에 없고 ADC의 실제 성능을 평가하기 위한 다른 지표들이 있다. SINAD, ENOB, THD+N 와 같은... 이에 대해서는 다음번에 글을 올리도록 하겠다.
ADC SNR 공식
양자화 노이즈만을 고려한 이상적인 SNR값은 다음과 같이 구한다.
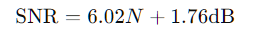
여기서 N은 ADC의 비트 수를 의미한다.
n bit ADC의 SNR 값
ADC의 비트 수에 따른 SNR 값은 다음과 같다.
예를 들어, 12비트 ADC는 74dB의 SNR 값을 갖는데, 이 값이 20*log10(S/N)임을 고려하면 양자화 잡음만을 고려한 이상적인 상황에서 신호의 세기가 노이즈에 비해 5012배 크다고 표현할 수 있다.
| Number of Bits (n) | SNR (dB) |
| 8 | 49.92 |
| 10 | 61.96 |
| 12 | 74 |
| 16 | 98.08 |
비트 수가 증가할수록 SNR 값도 같이 높아지는데, 이는 비트 분해능이 높은 ADC가 아날로그 신호를 더 촘촘하게 표현할 수 있기 때문에 당연한 결과이다.
하지만 실제 시스템에서도 고해상도 ADC가 저해상도 ADC보다 항상 잡음이 적고 신호를 정확하게 전달하냐고 하면 꼭 그렇지만은 않다. 외부 요인이 성능에 영향을 줄 수 있기 때문이다.
ADC SNR 공식 도출
그럼 이상적인 SNR 공식 6.02*n+1.06이 어떻게 유도되었는지 알아보자.
모든 ADC는 양자화로 인한 노이즈를 발생시킨다. 모든 아날로그 입력이 가장 가까운 디지털 레벨에 매핑되고, 해당 레벨과 입력의 실제 값의 차이가 노이즈로 간주되기 때문이다.
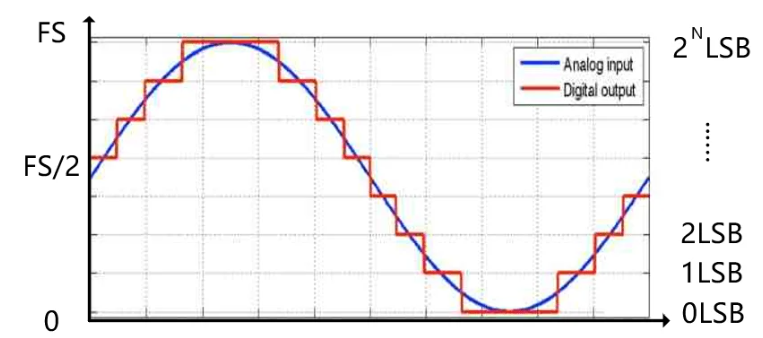
아래 그림과 같이 선형 아날로그 신호 입력에 대해 ADC는 계단형 출력을 생성한다.
이 때 양자화 간격(Qunatization Interval) q는 가장 작은 양자화 단계인 1 LSB(Least Significant Bit)이고 전압으로는 FS/2^n (여기서 FS은 ADC의 Full scale 입력 전압 범위)이다.
그리고 노이즈가 -q/2와 q/2 사이에서 균등하게 분포한다고 가정한다.

균등분포의 분산공식은 다음과 같은데 양자화 잡음의 분산을 계산하면 q^2/12이다. 그리고 표준편차는 분산의 제곱근 이므로 q/√12 이다.

즉 양자화 잡음의 RMS error는 q/√12가 된다. (평균이 0이라 가정하면 RMS(제곱평균제곱근)와 표준편차 계산식이 동일하다.)

SNR값은 신호의 실효값(RMS)을 잡음의 실효값(RMS)으로 나눈 뒤 상용로그를 취한 다음 20을 곱한 값인데 잡음의 실효값인 RMS noise는 위의 1번 공식에서 이미 구했으므로 이제 RMS signal만 구하면 된다.
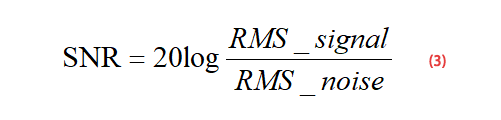
먼저 ADC 풀 스케일 전압 범위의 사인파 입력이 있다고 가정하자. 입력 신호는 A*sin(t)이고 여기서 A는 사인파의 진폭인데 범위가 0에서 부터 q*2^n이니까 이 범위의 절반인 q*2^n/2가 A가 된다.
그리고 sine wave의 실효값은 (진폭/√2) 이라서 결국 RMS signal을 5번 공식과 같이 알 수 있다.
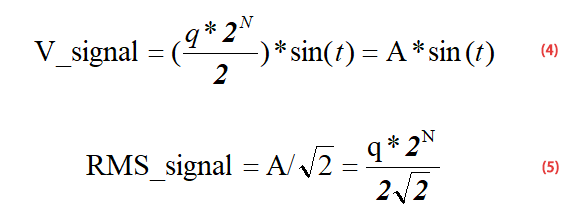
이제는 RMS signal과 RMS noise를 위 3번 공식에 대입하는 것만 남았다.
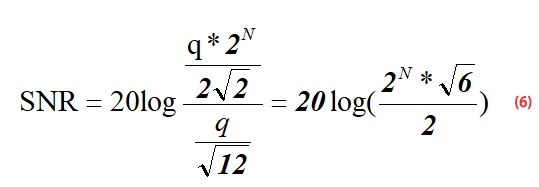
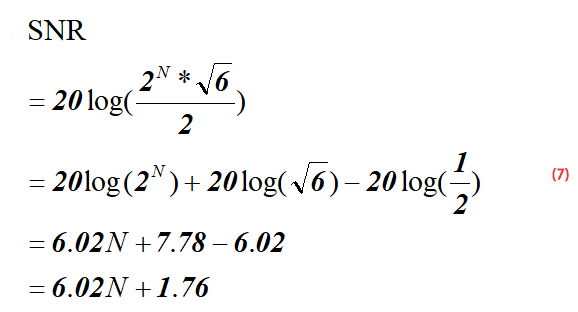
그리고 계산하면 SNR = 6.02*n+1.76 이라는 공식이 도출된다.
참고 : https://reversepcb.com/what-is-signal-to-noise-ratio-snr/